Metode Pencarian dan Pelacakan 2 (Heuristik)
Heuristik adalah sebuah teknik yang mengembangkan efisiensi dalam proses pencarian, namum dengan kemungkinan mengorbankan kelengkapan (completeness).
5.1 PENCARIAN TERBAIK PERTAMA(Best-First Search)
Metode ini merupakan kombinasi dari metode depth-first search dan breadth-first search. Pada metode best-first search, pencarian diperbolehkan mengunjungi node yang ada di level yang lebih rendah, jika ternyata node pada level yang lebih tinggi ternyata memiliki nilai heuristic yang lebih buruk.
Contoh :
5.2 Problem Reduction
Anggap A < B adalah constraint antara variabel A dengan domainDA = { 3..7} dan variabel B dengan domain DB = { 1..5}. dengan jelas tampak bahwa bahwa untuk sebagian nilai pada DA tidak ada nilai yang konsisten di DB yang memenuhi constraint A < B dan sebaliknya. Niai yang demikian dapat dibuang dari domain yang berkaitan tanpa kehilangan solusi apapun. Reduksi itu aman. Didapatkan domain yang tereduksi DA = {3,4} dan DB = {4,5}.
Kebanyakan solusi menggunakan pohonOR,dimana lintasan dari awal sampai tujuan tidak terletak pada satu cabang. Bila lintasan dari keadaan awal sampai tujuan dapat terletak pada satu cabang, maka kita akan dapat menemukan tujuan lebih cepat.
Graf AND-OR
Pada dasarnya sama dengan algoritma Best First Search, dengan mempertimbangkan adanya arc AND. Gambar berikut menunjukkan bahwa untuk mendapatkan TV orang bisa dengan cara singkat yaitu mencuri atau membeli asal mempunyai uang.Untuk mendeskripsikan algoritma, digunakan nilai F_UTILITY untuk biaya solusi.
Untuk mendeskripsikan algoritma Graph AND-OR kita menggunakan nilai F_UTILITY, yaitu biaya solusi.
1. Inisialisasi graph ke node awal.
Algoritma AO* menggunakan struktur Graph. Tiap-tiap node pada graph tersebut akan memiliki nilai h’ yang merupakan biaya estimasi jalur dari node itu sendiri sampai suatu solusi.
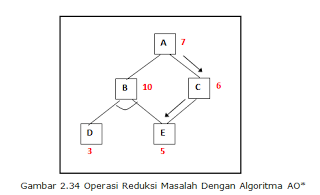
Sebagai contoh, pada Gambar 2.34 Jelas bahwa jalur melalui C selalu lebih baik daripada melalui B. Tetapi jika biaya node E muncul, dan pengaruh perubahan yang diberikan ke node B tidak sebesar pengaruhnya terhadap node C, maka jalur melalui B bisa jadi lebih baik. Sebagai contoh, hasil expand node E, misalkan 10, maka biaya node C menjadi 11 (10+1), dengan demikian biaya node A apabila memilih jalur lewat C adalah 12 (11+1). Tentu saja akan lebih baik memilih jalur melalui node B (11). Tapi tidak demikian halnya apabila kemudian node D diekspan. Bisa jadi jalur dengan melalui node B akan lebih buruk lagi ketimbang jalur dengan melalui node C.
5.3 Constraint Satisfaction
Problem search standart
- state adalah "black box“
- setiap struktur data yang mendukung fungsi successor, fungsi heuristik dan tes goal.
CSP
- state didefinisikan sebagai variabel Xi dengan nilai dari domain Di – Tes goal adalah sekumpulan constraint yang menspesifikasikan kombinasi dari nilai subset variabel.
Contoh sederhana adalah bahasa representasi formal.
CSP ini merupakan algoritma general-purpose dengan kekuatan lebih daripada algoritma pencarian standar.
Contoh : Pewarnaan Peta
Variabel WA, NT, Q, NSW, V, SA, T
Domain Di = {red,green,blue}
Constraints : daerah yang bertetangga dekat harus memiliki warna yang berbeda.
Contoh WA ≠ NT, atau (WA,NT) {(red,green),(red,blue),(green,red), (green,blue),(blue,red),(blue,green)}
Constraints : daerah yang bertetangga dekat harus memiliki warna yang berbeda.
Contoh WA ≠ NT, atau (WA,NT) {(red,green),(red,blue),(green,red), (green,blue),(blue,red),(blue,green)}
Solusi lengkap dan konsisten, contoh : WA = red, NT = green,Q = red,NSW = green,V = red,SA = blue,T = green
Constraint Graf
Binary CSP biner : setiap constraint merelasikan dua variable
Graf Constraint : node adalah variabel, arc adalah constraint
Graf Constraint : node adalah variabel, arc adalah constraint
5.4 Means End Analysis
MEA adalah strategi penyelesaian masalah yang diperkenalkan pertama kali dalam GPS (General Problem Solver) [Newell & Simon, 1963]. Proses pencarian berdasarkan ruang masalah yang menggabungkan aspek penalaran forward dan backward. Perbedaan antara state current dan goal digunakan untuk mengusulkan operator yang mengurangi perbedaan itu. Keterhubungan antara operator dan perbedaan tsb disajikan sebagai pengetahuan dalam sistem (pada GPS dikenal dengan Table of Connections) atau mungkin ditentukan sampai beberapa pemeriksaan operator jika tindakan operator dapat dipenetrasi.
Contoh OPERATOR first-order predicate calculus dan operator2 tertentu mengijinkan perbedaan korelasi task-independent terhadap operator yang menguranginya. Kapan pengetahuan ada tersedia mengenai pentingnya perbedaan, perbedaan yang paling utama terpilih pertama lebih lanjut meningkatkan rata-rata capaian dari MEA di atas strategi pencarian Brute-Force. Bagaimanapun, bahkan tanpa pemesanan dari perbedaan menurut arti penting, MEA meningkatkan metode pencarian heuristik lain (di rata-rata kasus) dengan pemusatan pemecahan masalah pada perbedaan yang nyata antara current state dengan goal-nya.
SUMBER:
REPRESENTASI PENGETAHUAN
Pengetahuan
Pengetahuan dibedakan menjadi 3 klasifikasi yaitu:
1. Prodecural Knowledge adalah pengetahuan yang berkaitan dengan prosedur atau cara untuk melakukan sesuatu. Contohnya, bagaimana cara mendidihkan air dalam panci.
2. Declarative Knowledge adalah pengetahuan untuk dapat menentukan nilai benar dan salah suatu hal. Contohnya, jangan celupkan tangan anda dalam air yang mendidih.
3. Tacid Knowledge kadang disebut juga sebagai "unconscious knowledge", karena pengetahuan tidak dapat diekspresikan atau didefinisikan dengan bahasa. Contohnya, bagaimana menggerakkan tangan.
6.1 Arti Pengetahuan
Pengetahuan (knowledge) adalah sesuatu yang hadir dan terwujud dalam jiwa dan pikiran seseorang karena adanya reaksi, sentuhan, dan hubungan dengan lingkungan dan alam sekitarnya. Pengetahuan adalah fakta atau keadaan yang timbul karena suatu pengalaman.
Contoh:
Representasi Pengetahuan
1. Representasi logika. Representasi jenis ini menggunakan ekspresi-ekspresi dalam logika formal untuk merepresentasikan basis pengetahuan.
2. Representasi prosedural. Representasi yang menggambarkan pengetahuan sebagai kumpulan instruksi untuk memecahkan suatu problema.
3. Representasi network. Representasi ini menangkap pengetahuan sebagai sebuah graf dimana simpul-simpulnya menggambarkan obyek atau konsep dari problema yang dihadapi, sedangkan edgenya menggambarkan hubungan atau asosiasi antar mereka.
4. Representasi terstruktur. Representasi terstruktur memperluas network dengan cara membuat setiap simpulnya menjadi struktur data kompleks.
Adapun bentuk representasi pengetahuan yang telah dikembangkan, yaitu :
6.2 PRODUKSI
Sistem produksi memiliki struktur seperti struktur proses pencarian (search).
6.3 Jaringan Semantik ( Semantic nets)
Jaringan Semantik adalah tehnik representasi dalam artificial intelligence klasik untuk informasi proposional, sehingga sering kali disebut sebagai poporsional network. Proposisi adalah pernyataan yang dapat bernilai benar atau salah dan merupakan bentuk pengetahuan deklaratif. Semantic network pertama kali dikembangkan untuk AI (Artificial Intelligence) sebagai cara untuk mempresentasikan memory dan pemahaman bahasa manusia. Struktur semantic nets berupa grafik dengan node (simpul) dan arc (ruas) yang menghubungkannya.
- Representasi grafis dari informasi Propositional.
- Proposisi adalah pernyataan yang dapat bernilai benar atau salah.
- Disajikan dalam bentuk graf berarah
- Node merepresentasikan konsep, objek atau situasi :
• Label ditunjukkan melalui penamaan
• Node dapat berupa objek tunggal atau kelas
- Links merepresentasikan suatu hubungan :
• Links adalah struktur dasar untuk pengorganisasian pengetahuan
• Contoh jaringan semantic.
Berikut ini adalah contoh sebuah jaringan semantik :
2. Donat bentuknya bulat
3. Dessi punya adik namanya sendi
4. Sendi pergi sekolah naik motor
5. Sendi pergi sekolah membawa bola
6. Dessi bermain bola
7. Bola bentuknya bulat
8. Motor membutuhkan bensin
9. Pom bensin menyediakan bensin
10. Sendi punya rumah dekat pom bensin
6.4 Triple Obyek-Atribut-Nilai
Bentuk object-attribute-value triple dapat digunakan untuk mempresentasikan semua karakteristik pengetahuan dalam semantic net dan digunakan pada sistem pakar MYCIN untuk mendiagnosa penyakit infeksi.
6.5 Schemata : Frame dan Script
Salah satu tipe skema yang digunakan dalam beberapa aplikasi AI adalah frame. Frame merupakan struktur yang baik untuk mempresentasikan objek yang tipikal dalam situasi tertentu. Karakteristik dasar frame adalah frame mempresentasikan pengetahuan yang terkait mengenai sebuah subjek yang sempit dan memiliki default. Sistem frame adalah pilihan yang baik untuk mendeskripsikan peralatan mekanik seperti mobil. Frame mencoba memodelkan obyek yang ada di dunia nyata menggunakan pengetahuan generik untuk atribut yang banyak dimiliki oleh obyek dan pengetahuan spesifik untuk kasus khusus.
SUMBER:
Pengetahuan
Pengetahuan dibedakan menjadi 3 klasifikasi yaitu:
1. Prodecural Knowledge adalah pengetahuan yang berkaitan dengan prosedur atau cara untuk melakukan sesuatu. Contohnya, bagaimana cara mendidihkan air dalam panci.
2. Declarative Knowledge adalah pengetahuan untuk dapat menentukan nilai benar dan salah suatu hal. Contohnya, jangan celupkan tangan anda dalam air yang mendidih.
3. Tacid Knowledge kadang disebut juga sebagai "unconscious knowledge", karena pengetahuan tidak dapat diekspresikan atau didefinisikan dengan bahasa. Contohnya, bagaimana menggerakkan tangan.
6.1 Arti Pengetahuan
Pengetahuan (knowledge) adalah sesuatu yang hadir dan terwujud dalam jiwa dan pikiran seseorang karena adanya reaksi, sentuhan, dan hubungan dengan lingkungan dan alam sekitarnya. Pengetahuan adalah fakta atau keadaan yang timbul karena suatu pengalaman.
Contoh:
Pengetahuan tentang binatang, sifat-sifat dan perilakunya. Pengetahuan tentang penyakit,gejala-gejala dan pengobatan nya. Pengetahuan tentang tanaman.jenis-jenisnya dan cara hidupnya dan lain-lain.
Representasi Pengetahuan
Representasi pengetahuan adalah suatu teknik untuk merepresentasikan basis pengetahuan yang diperoleh ke dalam suatu skema/diagram tertentu sehingga dapat diketahui relasi/keterhubungan antara suatu data dengan data yang lain sehingga dapat diuji kebenaran penalarannya. Representasi pengetahuan biasanya digunakan untuk pembuatan sistem pakar di mana komputer dirancang untuk dapat mengambil keputusan seperti manusia agar dapat memecahkan permasalahan. Secara singkat, representasi pengetahuan diklarifikasikan menjadi 4 kategori :
1. Representasi logika. Representasi jenis ini menggunakan ekspresi-ekspresi dalam logika formal untuk merepresentasikan basis pengetahuan.
2. Representasi prosedural. Representasi yang menggambarkan pengetahuan sebagai kumpulan instruksi untuk memecahkan suatu problema.
3. Representasi network. Representasi ini menangkap pengetahuan sebagai sebuah graf dimana simpul-simpulnya menggambarkan obyek atau konsep dari problema yang dihadapi, sedangkan edgenya menggambarkan hubungan atau asosiasi antar mereka.
4. Representasi terstruktur. Representasi terstruktur memperluas network dengan cara membuat setiap simpulnya menjadi struktur data kompleks.
Adapun bentuk representasi pengetahuan yang telah dikembangkan, yaitu :
6.2 PRODUKSI
Sistem produksi memiliki struktur seperti struktur proses pencarian (search).
Secara umum, sistem produksi terdiri dari komponen-komponen:
Ruang Keadan : berisi keadaan awal, tujuan dan kumpulan aturan yang digunakan untuk mencapai tujuan.
Memori Aktif : berisi deskripsi keadaan semesta pembicaraan saat ini dalam proses penalaran.
Strategi Kontrol : berguna untuk mengarahkan bagaimana proses pencarian akan berlangsung dan mengendalikan arah eksplorasi.
Representasi pengetahuan dengan sistem produksi dinamakan kaidah/aturan produksi (production method) sering disebut produksi saja.
6.3 Jaringan Semantik ( Semantic nets)
Jaringan Semantik adalah tehnik representasi dalam artificial intelligence klasik untuk informasi proposional, sehingga sering kali disebut sebagai poporsional network. Proposisi adalah pernyataan yang dapat bernilai benar atau salah dan merupakan bentuk pengetahuan deklaratif. Semantic network pertama kali dikembangkan untuk AI (Artificial Intelligence) sebagai cara untuk mempresentasikan memory dan pemahaman bahasa manusia. Struktur semantic nets berupa grafik dengan node (simpul) dan arc (ruas) yang menghubungkannya.
- Dibangun oleh M.R.Quillian, sebagai model memori manusia.
- Representasi grafis dari informasi Propositional.
- Proposisi adalah pernyataan yang dapat bernilai benar atau salah.
- Disajikan dalam bentuk graf berarah
- Node merepresentasikan konsep, objek atau situasi :
- Representasi grafis dari informasi Propositional.
- Proposisi adalah pernyataan yang dapat bernilai benar atau salah.
- Disajikan dalam bentuk graf berarah
- Node merepresentasikan konsep, objek atau situasi :
• Label ditunjukkan melalui penamaan
• Node dapat berupa objek tunggal atau kelas
- Links merepresentasikan suatu hubungan :
• Links adalah struktur dasar untuk pengorganisasian pengetahuan
• Contoh jaringan semantic.
Contoh Jaringan Semantik dalam Representasi Pengetahuan
Jaringan semantik merupakan model memori manusia yang dibangun oleh M. R. Quillian sebagai representasi grafis dari informasi proposisional. Informasi proposisional adalah pernyataan yang dapat bernilai benar atau salah. Jaringan semantik ini disajikan dalam bentuk graf berarah.
Berikut ini adalah contoh sebuah jaringan semantik :
Berikut ini adalah contoh sebuah jaringan semantik :
Informasi proposisional yang membentuk jaringan semantik di atas adalah :
1. Dessi makan donat
2. Donat bentuknya bulat
3. Dessi punya adik namanya sendi
4. Sendi pergi sekolah naik motor
5. Sendi pergi sekolah membawa bola
6. Dessi bermain bola
7. Bola bentuknya bulat
8. Motor membutuhkan bensin
9. Pom bensin menyediakan bensin
10. Sendi punya rumah dekat pom bensin
2. Donat bentuknya bulat
3. Dessi punya adik namanya sendi
4. Sendi pergi sekolah naik motor
5. Sendi pergi sekolah membawa bola
6. Dessi bermain bola
7. Bola bentuknya bulat
8. Motor membutuhkan bensin
9. Pom bensin menyediakan bensin
10. Sendi punya rumah dekat pom bensin
6.4 Triple Obyek-Atribut-Nilai
Bentuk object-attribute-value triple dapat digunakan untuk mempresentasikan semua karakteristik pengetahuan dalam semantic net dan digunakan pada sistem pakar MYCIN untuk mendiagnosa penyakit infeksi.
6.5 Schemata : Frame dan Script
Salah satu tipe skema yang digunakan dalam beberapa aplikasi AI adalah frame. Frame merupakan struktur yang baik untuk mempresentasikan objek yang tipikal dalam situasi tertentu. Karakteristik dasar frame adalah frame mempresentasikan pengetahuan yang terkait mengenai sebuah subjek yang sempit dan memiliki default. Sistem frame adalah pilihan yang baik untuk mendeskripsikan peralatan mekanik seperti mobil. Frame mencoba memodelkan obyek yang ada di dunia nyata menggunakan pengetahuan generik untuk atribut yang banyak dimiliki oleh obyek dan pengetahuan spesifik untuk kasus khusus.
SUMBER:
http://meldhycom.blogspot.co.id/2013/06/representasi-pengetahuan-sistem.html
Representasi Pengetahuan : Logika Proposisi
7.1 Logika dan Set
– Union (Gabungan)
– Komplemen
7.2 Operator Logika
Tabel Kebenaran Logika
Predicate Logic (Logika Predikat)
Mencintai (Bu Atika, Pak Agus Setiawan)
Contoh Silsilah Keluarga yang dipresentasikan dalam Prolog
Jika silsilah di atas dibentuk dalam Representasi Logika, sebagai berikut:
7.3 Tautologi, Kontradiksi dan Contingent
Adalah suatu ekspresi logika yang selalu bernilai benar di dalam tabel kebenarannya, tanpa memperdulikan nilai kebenaran dari proposisi-proposisi yang berada didalamnya.
Kontradiksi
Adalah proposisi komposit yang selalu bernilai salah untuk setiap nilai kebenaran dari proposisi elementernya.
Contingent
Adalah proposisi komposit yang bukan tautologi dan kontradiksi.
7.4 Resolusi Logika Proposisi
Resolusi merupakan suatu teknik pembuktian yang lebih efisien, sebab fakta-fakta yang akan dioperasikan terlebih dahulu dibawa ke bentuk standar yang sering disebut dengan nama klausa. Pembuktian suatu pernyataan menggunakan resolusi ini dilakukan dengan cara menegasikan pernyataan tersebut, kemudian dicari kontradiksinya dari pernyataan-pernyataan yang sudah ada.
Resolusi adalah suatu aturan untuk melakukan inferensi yang dapat berjalan secara efisien dalam suatu bentuk khusus conjunctive normal form (CNF). Pada logika proposisi, prosedur untuk membuktikan proposisi P dengan beberapa aksioma F yang telah diketahui, dengan menggunakan resolusi.
Algoritma resolusi :
(1) Konversikan semua proposisi F ke bentuk CNF.
(2) Negasikan P, dan konversikan hasil negasi tersebut ke bentuk klausa. Tambahkan ke himpunan klausa yang telah ada pada langkah 1.
(3) Kerjakan hingga terjadi kontradiksi atau proses tidak mengalami kemajuan :
a. Seleksi 2 klausa sebagai klausa parent.
b. Bandingkan (resolve) secara bersama-sama. Klausa hasil resolve tersebut dinamakan resolvent. Jika ada pasangan literal L dan ¬L, eliminir dari resolvent.
c. Jika resolvent berupa klausa kosong, maka ditemukan kontradiksi. Jika tidak, tambahkan ke himpunan klausa yang telah ada.
Contoh :
Diketahui basis pengetahuan (fakta-fakta yang bernilai benar) sebagai berikut:
1. P
2. (P ∧ Q) → R
3. (S ∨ T) → Q
4. T
Buktikanlah kebenaran R!
Pertama-tama kita harus ubah dulu keempat fakta di atas menjadi bentuk CNF. Konversi ke CNF dapat dilakukan sebagai berikut:
Kemudian kita tambahkan kontradiksi pada tujuannya, R menjadi ¬R sehingga fakta-fakta (dalam bentuk CNF) dapat disusun menjadi:
1. P
2. ¬P ∨ ¬Q ∨ R
3. ¬S ∨ Q
4. ¬T ∨ Q
5. T
6. ¬R
Dengan demikian resolusi dapat dilakukan untuk membuktikan R sebagaimana terlihat pada Gambar berikut:
Contoh apabila diterapkan dalam kalimat:
P : Andi anak yang cerdas.
Q : Andi rajin belajar.
R : Andi akan menjadi juara kelas.
S : Andi makannya banyak.
T : Andi istirahatnya cukup.
Kalimat yang terbentuk (basis pengetahuan) menjadi :
1. P : Andi anak yang cerdas.
2. (P ∧ Q) → R : Jika Andi anak yang cerdas dan Andi rajin belajar, maka Andi akan menjadi juara kelas.
3. (S ∨ T) → Q : Jika Andi makannya banyak atau Andi istirahatnya cukup, maka Andi rajin belajar.
4. T : Andi istirahatnya cukup.
Setelah dilakukan konversi ke bentuk CNF, didapat:
1. P : Andi anak yang cerdas.
2. ¬P ∨ ¬Q ∨ R : Andi tidak cerdas atau Andi tidak rajin belajar atau Andi akan menjadi juara kelas.
3. ¬S ∨ Q : Andi tidak makan banyak atau Andi rajin belajar.
4. ¬T ∨ Q : Andi tidak cukup istirahat atau Andi rajin belajar.
5. T : Andi istirahatnya cukup.
6. ¬R : Andi tidak akan menjadi juara kelas.
Pohon aplikasi resolusi untuk kejadian di atas sebagai berikut :
Sumber:
7.1 Logika dan Set
Representasi pengetahuan dengan symbol logika merupakan bagian dari penalaran eksak.Merupakan bagian yang paling penting dalam penalaran adalah mengambil kesimpulan dari premis. Dan Logika dikembangkan oleh filusuf Yunani, Aristoteles (abad ke 4 SM) didasarkan pada silogisme, dengan dua premisdan satu konklusi.
Contoh :
– Premis : Semua wanita adalah makhluk hidup
– Premis : Milan adalah wanita
– Konklusi : Milan adalah makhluk hidup
Cara lain merepresentasikan pengetahuan adalah dengan Diagram Venn.
Diagram Venn merepresentasikan sebuah himpunan yang merupakan kumpulan objek. Objek dalam himpunan disebut elemen.
A ={1,3,5,7} , B = {….,-4,-2,0,2,4,…..} , C = {pesawat, balon}
Symbol epsilon ε menunjukkan bahwa suatu elemen merupakan anggota dari suatu himpunan, contoh : 1 ε A . Jika suatu elemen bukan anggota dari suatu himpunan maka symbol yang digunakan ∉, contoh : 2 ∉ A.Jika suatu himpunan sembarang, misal X dan Y didefinisikan bahwa setiap elemen X merupakan elemen Y, maka X adalah subset dari Y, dituliskan : X ⊂ Y atau Y ⊃ X.
Operasi-operasi Dasar dalam Diagram Venn:
– Interseksi (Irisan)
C = A ∩ B C = {x ∈ U | (x ∈ A) ∧ (x ∈ B)}
Dimana : ∩ menyatakan irisan himpunan | dibaca “sedemikian hingga” ∧ operator logika AND
– Union (Gabungan)
C = A ∪ B C = {x ∈ U | (x ∈ A) ∨ (x ∈ B)}
Dimana : ∪ menyatakan gabungan himpunan operator logika OR
– Komplemen
A’ = {x ∈ U | ~(x ∈ A) }
Dimana : ’ menyatakan komplemen himpunan ~ operator logika NOT
7.2 Operator Logika
Logika didefinisikan sebagai ilmu untuk berpikir dan menalar dengan benar sehingga didapatkan kesimpulan yang absah.
Tujuan dari logika: memberikan aturan-aturan penalaran sehingga orang dapat menentukan apakah suatu kalimat bernilai benar atau salah.
Representasi Logika dibagi menjadi dua:
Propositional Logic (Logika Proposisi)
Suatu Proposisi merupakan suatu statemen atau pernyataan yang menyatakan benar (TRUE) atau salah (FALSE). Dalam PropositionalLogic fakta dilambangkan dengan simbol misalnya P, Q dan R.Lambang-lambang tersebut dihubungkan dengan relasi-relasi logika
Dengan menggunakan operator logika:
Tabel Kebenaran Logika
Predicate Logic (Logika Predikat)
Pada logika predikat proposisi dibedakan menjadi argumen (obyek) dan predikat (keterangan). Secara umum penulisan proposisi dalam logika predikat dapat dinyatakan sebagai berikut:
Predikat (argumen-1, argumen-2,..., argumen-3)
Contoh:
Proposisi: “Bu Atika mencintai Pak Agus Setiawan”
Dalam logika predikat disajikan dalam bentuk:
Mencintai (Bu Atika, Pak Agus Setiawan)
P Argumen-1 Argumen-2
Contoh Silsilah Keluarga yang dipresentasikan dalam Prolog
Jika silsilah di atas dibentuk dalam Representasi Logika, sebagai berikut:
Orangtua (Komarudin, Andika)
Orangtua (Komarudin, Atika)
Orangtua (Komarudin, Agus)
Orangtua (Andika, Rika)
Orangtua (Atika, Anjar)
7.3 Tautologi, Kontradiksi dan Contingent
TAUTOLOGI
Adalah suatu ekspresi logika yang selalu bernilai benar di dalam tabel kebenarannya, tanpa memperdulikan nilai kebenaran dari proposisi-proposisi yang berada didalamnya.
Contoh : pv(→p) selalu bernilai benar.
Kontradiksi
Adalah proposisi komposit yang selalu bernilai salah untuk setiap nilai kebenaran dari proposisi elementernya.
Contoh : (~p V ~Q) ßà(P&Q) selalu bernilai salah.
Contingent
Adalah proposisi komposit yang bukan tautologi dan kontradiksi.
Contoh [(p^q)à r ] à p
7.4 Resolusi Logika Proposisi
Resolusi merupakan suatu teknik pembuktian yang lebih efisien, sebab fakta-fakta yang akan dioperasikan terlebih dahulu dibawa ke bentuk standar yang sering disebut dengan nama klausa. Pembuktian suatu pernyataan menggunakan resolusi ini dilakukan dengan cara menegasikan pernyataan tersebut, kemudian dicari kontradiksinya dari pernyataan-pernyataan yang sudah ada.
Resolusi adalah suatu aturan untuk melakukan inferensi yang dapat berjalan secara efisien dalam suatu bentuk khusus conjunctive normal form (CNF). Pada logika proposisi, prosedur untuk membuktikan proposisi P dengan beberapa aksioma F yang telah diketahui, dengan menggunakan resolusi.
Algoritma resolusi :
(1) Konversikan semua proposisi F ke bentuk CNF.
(2) Negasikan P, dan konversikan hasil negasi tersebut ke bentuk klausa. Tambahkan ke himpunan klausa yang telah ada pada langkah 1.
(3) Kerjakan hingga terjadi kontradiksi atau proses tidak mengalami kemajuan :
a. Seleksi 2 klausa sebagai klausa parent.
b. Bandingkan (resolve) secara bersama-sama. Klausa hasil resolve tersebut dinamakan resolvent. Jika ada pasangan literal L dan ¬L, eliminir dari resolvent.
c. Jika resolvent berupa klausa kosong, maka ditemukan kontradiksi. Jika tidak, tambahkan ke himpunan klausa yang telah ada.
Contoh :
Diketahui basis pengetahuan (fakta-fakta yang bernilai benar) sebagai berikut:
1. P
2. (P ∧ Q) → R
3. (S ∨ T) → Q
4. T
Buktikanlah kebenaran R!
Pertama-tama kita harus ubah dulu keempat fakta di atas menjadi bentuk CNF. Konversi ke CNF dapat dilakukan sebagai berikut:
Resolusi adalah suatu aturan untuk melakukan inferensi yang dapat berjalan secara efisien dalam suatu bentuk khusus conjunctive normal form (CNF). Pada logika proposisi, prosedur untuk membuktikan proposisi P dengan beberapa aksioma F yang telah diketahui, dengan menggunakan resolusi.
Algoritma resolusi :
(1) Konversikan semua proposisi F ke bentuk CNF.
(2) Negasikan P, dan konversikan hasil negasi tersebut ke bentuk klausa. Tambahkan ke himpunan klausa yang telah ada pada langkah 1.
(3) Kerjakan hingga terjadi kontradiksi atau proses tidak mengalami kemajuan :
a. Seleksi 2 klausa sebagai klausa parent.
b. Bandingkan (resolve) secara bersama-sama. Klausa hasil resolve tersebut dinamakan resolvent. Jika ada pasangan literal L dan ¬L, eliminir dari resolvent.
c. Jika resolvent berupa klausa kosong, maka ditemukan kontradiksi. Jika tidak, tambahkan ke himpunan klausa yang telah ada.
Contoh :
Diketahui basis pengetahuan (fakta-fakta yang bernilai benar) sebagai berikut:
1. P
2. (P ∧ Q) → R
3. (S ∨ T) → Q
4. T
Buktikanlah kebenaran R!
Pertama-tama kita harus ubah dulu keempat fakta di atas menjadi bentuk CNF. Konversi ke CNF dapat dilakukan sebagai berikut:
Kemudian kita tambahkan kontradiksi pada tujuannya, R menjadi ¬R sehingga fakta-fakta (dalam bentuk CNF) dapat disusun menjadi:
1. P
2. ¬P ∨ ¬Q ∨ R
3. ¬S ∨ Q
4. ¬T ∨ Q
5. T
6. ¬R
Dengan demikian resolusi dapat dilakukan untuk membuktikan R sebagaimana terlihat pada Gambar berikut:
1. P
2. ¬P ∨ ¬Q ∨ R
3. ¬S ∨ Q
4. ¬T ∨ Q
5. T
6. ¬R
Dengan demikian resolusi dapat dilakukan untuk membuktikan R sebagaimana terlihat pada Gambar berikut:
Contoh apabila diterapkan dalam kalimat:
P : Andi anak yang cerdas.
Q : Andi rajin belajar.
R : Andi akan menjadi juara kelas.
S : Andi makannya banyak.
T : Andi istirahatnya cukup.
Kalimat yang terbentuk (basis pengetahuan) menjadi :
1. P : Andi anak yang cerdas.
2. (P ∧ Q) → R : Jika Andi anak yang cerdas dan Andi rajin belajar, maka Andi akan menjadi juara kelas.
3. (S ∨ T) → Q : Jika Andi makannya banyak atau Andi istirahatnya cukup, maka Andi rajin belajar.
4. T : Andi istirahatnya cukup.
Setelah dilakukan konversi ke bentuk CNF, didapat:
1. P : Andi anak yang cerdas.
2. ¬P ∨ ¬Q ∨ R : Andi tidak cerdas atau Andi tidak rajin belajar atau Andi akan menjadi juara kelas.
3. ¬S ∨ Q : Andi tidak makan banyak atau Andi rajin belajar.
4. ¬T ∨ Q : Andi tidak cukup istirahat atau Andi rajin belajar.
5. T : Andi istirahatnya cukup.
6. ¬R : Andi tidak akan menjadi juara kelas.
Pohon aplikasi resolusi untuk kejadian di atas sebagai berikut :
P : Andi anak yang cerdas.
Q : Andi rajin belajar.
R : Andi akan menjadi juara kelas.
S : Andi makannya banyak.
T : Andi istirahatnya cukup.
Kalimat yang terbentuk (basis pengetahuan) menjadi :
1. P : Andi anak yang cerdas.
2. (P ∧ Q) → R : Jika Andi anak yang cerdas dan Andi rajin belajar, maka Andi akan menjadi juara kelas.
3. (S ∨ T) → Q : Jika Andi makannya banyak atau Andi istirahatnya cukup, maka Andi rajin belajar.
4. T : Andi istirahatnya cukup.
Setelah dilakukan konversi ke bentuk CNF, didapat:
1. P : Andi anak yang cerdas.
2. ¬P ∨ ¬Q ∨ R : Andi tidak cerdas atau Andi tidak rajin belajar atau Andi akan menjadi juara kelas.
3. ¬S ∨ Q : Andi tidak makan banyak atau Andi rajin belajar.
4. ¬T ∨ Q : Andi tidak cukup istirahat atau Andi rajin belajar.
5. T : Andi istirahatnya cukup.
6. ¬R : Andi tidak akan menjadi juara kelas.
Pohon aplikasi resolusi untuk kejadian di atas sebagai berikut :
Sumber:
Representasi Pengetahuan Logika Predikat
Logika Predikat adalah perluasan dari logika proposisi dimana objek yang di bicarakan dapat berupa anggota kelompok. Misalkan P(x) merupakan sebuah pernyataan yang mengandung variabel x dan D adalah sebuah himpunan. Kita sebut P sebuah fungsi proposisi (dalam D) jika untuk setiap x di D, P(x) adalah proposisi. Kita sebut D daerah asal pembicaraan (domain of discourse) dari P.
8.1. FUNGSI FUNGSI LOGIKA PREDIKAT
Berikut ini beberapa contoh fungsi proposisi:
8.2. LOGIKA DAN SET ORDER PERTAMA
Logika Predikat Order Pertama disebut juga kalkulus predikat, merupakan logika yang digunakan untuk merepresentasikan masalah yang tidak dapat direpresentasikan dengan menggunakan proposisi. Logika predikat dapat memberikan representasi fakat-fakta sebagai suatu pernyataan yang mapan (well form).
Logika Predikat Order Pertama terdiri dari :
Konstanta: objek atau sifat dari semesta pembicaraan. Penulisannya diawali dengan huruf kecil, seperti : pohon, tinggi. Konstanta true(benar) dan false(salah) adalah symbol kebenaran (truth symbol).
Variable : digunakan untuk merancang kelas objek atau sifat-sifat secara umum dalam semesta pembicaraan. Penulisannya diawali dengan huruf besar, seperti : Bill, Kate.
Fungsi : pemetaan (mapping) dari satu atau lebih elemen dalam suatu himpunan yang disebut domainfungsi ke dalam sebuah elemen unik pada himpunan lain yang disebut rangefungsi. Penulisannya dimulai dengan huruf kecil. Suatu ekspresi fungsi merupakan symbol fungsi yang diikuti argument.
Argument adalah elemen-elemen dari fungsi, ditulis diapit tanda kurung dan dipisahkan dengan tanda koma.
Predikat: menamai hubungan antara nol atau lebih objek dalam semesta pembicaraan. Penulisannya dimulai dengan huruf kecil, seperti : equals, sama dengan, likes, near.
Contoh kalimat dasar :
teman(george,allen)
8.3. QUANTIFIER UNIVERSAL
Dalam logika predikat , quantifieri universal merupakan jenis quantifier , sebuah konstanta logis yang ditafsirkan sebagai “diberi” atau “untuk semua”. Ini mengungkapkan bahwa fungsi proposisi dapat dipenuhi oleh setiapanggota dari domain wacana. Dalam istilah lain, itu adalah predikasi dariproperti atau hubungan dengan setiap anggota domain. Ini menegaskanbahwa predikat dalam lingkup dari quantifier universal benar dari setiap nilai dari variabel predikat .
8.4. QUANTIFIER EXISTENSIAL
Dalam logika predikat , suatu quantifier eksistensial adalah jenis quantifier , sebuah konstanta logis yang ditafsirkan sebagai “ada ada,” “ada setidaknya satu,” atau “untuk beberapa.” Ini mengungkapkan bahwa fungsi proposisi dapat dipenuhi oleh setidaknya satu anggota dari domain wacana . Dalam istilah lain, itu adalah predikasi dari properti atau hubungan dengan setidaknya satu anggota dari domain. Ini menegaskan bahwa predikat dalamlingkup dari quantifier eksistensial adalah benar dari setidaknya satu nilai darivariabel predikat .
8.5. RESOLUSI LOGIKA PREDIKAT
Resolusi pada logika predikat pada dasarnya sama dengan resolusi pada logika proposisi, hanya saja ditambah dengan unifikasi.Pada logika predikat, prosedur untuk membuktikan pernyataan P dengan beberapa pernyataan F yang telah diketahui, dengan menggunakan resolusi, dapat dilakukan melalui algoritma sebagai berikut :
1. Konversikan semua proposisi F ke bentuk klausa
Contoh kasus :
Maka harus terlebih dahulu diubah ke dalam bentuk klausa sebagai berikut :
Sumber:
Logika Predikat adalah perluasan dari logika proposisi dimana objek yang di bicarakan dapat berupa anggota kelompok. Misalkan P(x) merupakan sebuah pernyataan yang mengandung variabel x dan D adalah sebuah himpunan. Kita sebut P sebuah fungsi proposisi (dalam D) jika untuk setiap x di D, P(x) adalah proposisi. Kita sebut D daerah asal pembicaraan (domain of discourse) dari P.
8.1. FUNGSI FUNGSI LOGIKA PREDIKAT
Berikut ini beberapa contoh fungsi proposisi:
n² + 2n adalah bilangan ganjil, dengan daerah asal himpunan bilangan bulat.
x² – x – 6 = 0, dengan daerah asal himpunan bilangan real.
Seorang pemain bisbol memukul bola melampaui 300 pada tahun 1974, dengan daerah asal himpunan pemain bisbol.
Sebuah predikat seringkali menyatakan sebuah hubungan relasional antara: konstanta, variabel dan fungsi.
8.2. LOGIKA DAN SET ORDER PERTAMA
Logika Predikat Order Pertama disebut juga kalkulus predikat, merupakan logika yang digunakan untuk merepresentasikan masalah yang tidak dapat direpresentasikan dengan menggunakan proposisi. Logika predikat dapat memberikan representasi fakat-fakta sebagai suatu pernyataan yang mapan (well form).
Logika orde pertama adalah sistem resmi yang digunakan dalam matematika , filsafat ,linguistik , dan ilmu komputer . Hal ini juga dikenal sebagai orde pertama predikat kalkulus, semakin rendah kalkulus predikat, teori kuantifikasi, dan logika predikat. Logika orde pertama dibedakan dari logika proposisional oleh penggunaan variabel terukur .
Syarat-syarat symbol dalam logika predikat :
himpunan huruf, baik huruf kecil maupun huruf besar dalam abjad.
Himpunan digit (angka) 0,1,2,…9
Garis bawah “_”
Symbol-simbol dalam logika predikat dimulai dengan sebuah huruf dan diikuti oleh sembarang rangkaian karakter-karakter yang diijinkan.
Symbol-simbol logika predikat dapat merepresentasikan variable, konstanta, fungsi atau predikat
Logika Predikat Order Pertama terdiri dari :
Konstanta: objek atau sifat dari semesta pembicaraan. Penulisannya diawali dengan huruf kecil, seperti : pohon, tinggi. Konstanta true(benar) dan false(salah) adalah symbol kebenaran (truth symbol).
Variable : digunakan untuk merancang kelas objek atau sifat-sifat secara umum dalam semesta pembicaraan. Penulisannya diawali dengan huruf besar, seperti : Bill, Kate.
Fungsi : pemetaan (mapping) dari satu atau lebih elemen dalam suatu himpunan yang disebut domainfungsi ke dalam sebuah elemen unik pada himpunan lain yang disebut rangefungsi. Penulisannya dimulai dengan huruf kecil. Suatu ekspresi fungsi merupakan symbol fungsi yang diikuti argument.
Argument adalah elemen-elemen dari fungsi, ditulis diapit tanda kurung dan dipisahkan dengan tanda koma.
Predikat: menamai hubungan antara nol atau lebih objek dalam semesta pembicaraan. Penulisannya dimulai dengan huruf kecil, seperti : equals, sama dengan, likes, near.
Contoh kalimat dasar :
teman(george,allen)
teman(ayah_dari(david),ayah_dari(andrew))
dimana:
argument : ayah_dari(david) adalah george
argument : ayah_dari(andrew) adalah allen
predikat : teman
8.3. QUANTIFIER UNIVERSAL
Dalam logika predikat , quantifieri universal merupakan jenis quantifier , sebuah konstanta logis yang ditafsirkan sebagai “diberi” atau “untuk semua”. Ini mengungkapkan bahwa fungsi proposisi dapat dipenuhi oleh setiapanggota dari domain wacana. Dalam istilah lain, itu adalah predikasi dariproperti atau hubungan dengan setiap anggota domain. Ini menegaskanbahwa predikat dalam lingkup dari quantifier universal benar dari setiap nilai dari variabel predikat .
Hal ini biasanya dilambangkan dengan berbalik A (∀) operator logika simbol, yang bila digunakan bersama-sama dengan variabel predikat, disebut quantifier universal (“∀x”, “∀ (x)”, atau kadang-kadang dengan “(x) “saja). Kuantifikasi Universal berbeda dari kuantifikasi eksistensial (“ada ada”), yang menegaskan bahwa properti atau relasi hanya berlaku untuk setidaknya satu anggota dari domain.
Contoh 1 :
(∀x) (x + x = 2x)
“untuk setiap x (dimana x adalah suatu bilangan), kalimat x + x = 2x adalah benar.”
Contoh 2 :
(∀x) (p) (Jika x adalah seekor kelinci -> x adalah binatang).
Kebalikan kalimat “bukan kelinci adalah binatang” ditulis :
(∀x) (p) (Jika x adalah seekor kelinci -> ~x adalah binatang)
dan dibaca :
– “setiap kelinci adalah bukan binatang”
“semua kelinci adalah bukan binantang”
8.4. QUANTIFIER EXISTENSIAL
Dalam logika predikat , suatu quantifier eksistensial adalah jenis quantifier , sebuah konstanta logis yang ditafsirkan sebagai “ada ada,” “ada setidaknya satu,” atau “untuk beberapa.” Ini mengungkapkan bahwa fungsi proposisi dapat dipenuhi oleh setidaknya satu anggota dari domain wacana . Dalam istilah lain, itu adalah predikasi dari properti atau hubungan dengan setidaknya satu anggota dari domain. Ini menegaskan bahwa predikat dalamlingkup dari quantifier eksistensial adalah benar dari setidaknya satu nilai darivariabel predikat .
Hal ini biasanya dilambangkan dengan E berubah (∃) operator logika simbol, yang bila digunakan bersama-sama dengan variabel predikat, disebut quantifier eksistensial (“∃x” atau “∃ (x)”) Kuantifikasi eksistensial.
Contoh 1 :
(∃x) (x . x = 1)
Dibaca : “terdapat x yang bila dikalikan dengan dirinya sendiri hasilnya sama dengan 1.”
Contoh 2 :
(∃x) (panda(x) ∧ nama(Clyde))
Dibaca : “beberapa panda bernama Clyde”.
Contoh 3 :
(∀x) (jerapah(x) -> berkaki empat(x))
Dibaca : “semua jerapah berkaki empat”.
Universal quantifier dapat diekspresikan sebagai konjungsi.
(∃x) (jerapahh(x) ∧ berkaki tiga(x))
Dibaca : “ada jerapah yang berkaki tiga”
Existensial quantifier dapat diekspresikan sebagai disjungsi dari
urutan ai. P(a1) ∨ P(a2) ∨ P(a3) …∨ P(aN)
8.5. RESOLUSI LOGIKA PREDIKAT
Resolusi pada logika predikat pada dasarnya sama dengan resolusi pada logika proposisi, hanya saja ditambah dengan unifikasi.Pada logika predikat, prosedur untuk membuktikan pernyataan P dengan beberapa pernyataan F yang telah diketahui, dengan menggunakan resolusi, dapat dilakukan melalui algoritma sebagai berikut :
1. Konversikan semua proposisi F ke bentuk klausa
2. Negasikan P, dan konversikan hasil negasi tersebut ke bentuk klausa.Tambahkan kehimpunan klausa yang telah ada pada langkah
3. Kerjakan hingga terjadi kontradiksi atau proses tidak mengalami kemajuan :
· Seleksi 2 klausa sebagai klausa parent
· Bandingkan (resolve) secara bersama-sama. Klausa hasil resolve tersebut resolvent. Jika ada pasangan literal T dan ¬T2 sedemikian hingga keduanya dapat dilakukan unifikasi, maka salah satu T1 dan T2 disebut sebagai complementary literal. Jika ada lebih dari 1 complementary literal, maka hanya sepasang yang dapat meninggalkan resolvent
· Jika resolvent berupa klausa kosong, maka ditemukan kontradiksi. Jika tidak, tambahkan ke himpunan klausa yang telah ada
Contoh kasus :
Misalkan terdapat pernyataan-pernyataan sebagai berikut :
1. Fajar adalah seorang mahasiswa
2. Fajar masuk Jurusan Elektro
3. Setiap mahasiswa elektro pasti mahasiswa Teknik
4. Kalkulus adalah matakuliah yang sulit
5. Setiap mahasiswa teknik pasti akan suka kalkulus atau akan membencinya
6. Setiap mahasiswa pasti akan suka terhadap suatu matakuliah
7. Mahasiswa yang tidak pernah hadir pada kuliah matakuliah sulit, maka mereka pasti tidak suka terhadap matakuliah tersebut
8. Fajar tidak pernah hadir kuliah matakuliah kalkulus
Maka harus terlebih dahulu diubah ke dalam bentuk klausa sebagai berikut :
1. Mahasiswa (Fajar)
2. Elektro (Fajar)
3.¬ Elektro (x1) v Teknik (v1)
4. Sulit (Kalkulus)
5.¬ Teknik (x2) v suka (x2, Kalkulus) v benci (x2, Kalkulus)
6. Suka (x3, f1 (x3))
7.¬ Mahasiswa (x4) v ¬ sulit (y1) v hadir (x4, y1) v ¬ suka (x4, y1)
8.¬ Hadir (Fajar, Kalkulus)
Sumber:


















Komentar
Posting Komentar